Introduction
Throughout youth sport, it is common practice to group children based on their age under the assumption that they will be similar in their development. Despite being born in the same calendar year, a child born in January will be nearly an entire year older than one born in December. These age differences can lead to the formation of relative age effects (RAEs). The RAE explains the relative (dis)advantages individuals experience because of where their birthdate falls compared to a pre-determined cut-off date. These (dis)advantages can, in turn, lead to a greater number of athletes born shortly after a cut-off date participating in a sport than their relatively younger counterparts (Barnsley et al., 1985). Moreover, athletes who are relatively older are more likely to continue in their sport to elite levels due to the developmental advantages they accumulate over time. For example, relatively older athletes may be selected to participate on better teams and receive more play and practice opportunities, due to them being more developed than their younger counterparts. On the contrary, relatively younger athletes are more likely to have negative sporting experiences, which can often lead to early drop out (Barnsley & Thompson, 1988; Delorme et al., 2010, 2011).
Researchers have studied RAEs within sport since the early 1980s and have found the phenomenon to be present in multiple sports, and across various levels of competition (Cobley et al., 2009). Despite a large body of RAE research, golf has garnered minimal attention by academics. In fact, there has not been any RAE research conducted on golfers at the intercollegiate level to date. Moreover, none of the previous RAE studies in golf have examined female golfers. Thus, this study will focus on areas previously unexamined by investigating the impact of the RAE, academic timing (AT), and choice of cut-off date among male and female golfers in the National Collegiate Athletic Association (NCAA).
Literature Review
Barnsley et al. (1985) examined the RAE in the National Hockey League (NHL) and in two Canadian development hockey leagues, the Western Hockey League (WHL) and the Ontario Hockey League (OHL). These authors found that there were four times as many players in the WHL and OHL born in the first quarter of the year (i.e., January, February, March) than in the fourth quarter (i.e., October, November, December). This trend was also reflected among NHL players, indicating a negative linear relationship between players’ birth months and their likelihood of reaching elite levels in the sport of hockey (Barnsley et al., 1985).
Since the initial work of Barnsley et al. (1985), a plethora of research has been conducted on the existence of RAEs in hockey. In particular, RAEs have been noted in subsequent studies involving NHL players e.g., (Addona & Yates, 2010; Côté et al., 2006; Daniel & Janssen, 1987), as well as in women’s hockey (Stenling & Holmström, 2014; Weir et al., 2010), youth hockey e.g., (Barnsley & Thompson, 1988; Hancock et al., 2013), interuniversity hockey (Chittle et al., 2015), and in French elite men’s hockey e.g., (Delorme et al., 2009). Other team sports that have been the focus of RAE studies include soccer e.g., (Augste & Lames, 2011; Cobley et al., 2008; Massa et al., 2014; Nakata & Sakamoto, 2011; Vincent & Gamser, 2006), basketball e.g., (Chittle et al., 2016; Delorme & Raspaud, 2009; Nakata & Sakamoto, 2011), baseball (Côté et al., 2006; Nakata & Sakamoto, 2011), softball (Dixon et al., 2013), volleyball, rugby (Roberts & Fairclough, 2012), and American and Canadian football e.g., (Chittle et al., 2018; Glamser & Marciani, 1992).
In addition to team sports, RAEs have also been noted in individual sports such as skiing (Baker et al., 2014; Müller et al., 2016), swimming (Costa et al., 2013), sprinting (Romann & Cobley, 2015), judo (Fukuda, 2015), tennis (Ulbricht et al., 2015), wrestling (Fukuda et al., 2017), as well as ekiden (long-distance relay races), and sumo (Nakata & Sakamoto, 2011). Historically, the RAE has been less studied in individual sports than in team sports. It was originally predicted that RAEs would not exist in individual sport contexts because of the lack of annual age groupings and/or the selection processes that occur within team sports (Cobley et al., 2009). However, as evidenced by the small sample of studies noted above, we know that RAEs may be prominent in both individual and team sports.
To date, there are only two known studies that have examined the RAE among golfers. The first study analyzed the birthdates of American golfers on the Professional Golfers’ Association (PGA) Tour using an August 1 cut-off date, which is consistent with the United States National Junior Championship that is held in the last two weeks of July (Côté et al., 2006). The results of Côté et al.'s (2006) study indicated no evidence of a RAE. These authors speculated that the absence of a RAE could be the result of organized golf starting at an older age than organized hockey or baseball, youth golf being less strict in its age groupings than other sports, and/or developmental factors such as height and weight being less likely to be influential in the sport. Subsequently, Nakata and Sakamoto (2011) studied Japanese male professional golfers from the Japan Golf Tour. Their results supported those of Côté et al. (2006), concluding that a RAE did not exist for this population either.
Academic Timing
When examining the RAE among intercollegiate athletes, an important factor to consider is academic timing (AT). First highlighted by Glamser and Marciani (1992), accounting for the AT of student-athletes is particularly important given that student-athletes commence university at differing ages, which can result in a wide age range of athletes competing against one another. With respect to AT, student-athletes may be grouped into one of three different categories based on their ages and athletic eligibilities: ‘on-time,’ ‘delayed,’ or ‘advanced.’ Student-athletes are considered ‘on-time’ when their athletic eligibilities correspond with their ages. However, if student-athletes are older than the age that corresponds with their athletic eligibility, they are categorized as ‘delayed,’ and if they are younger than the age that corresponds with their athletic eligibility, they are categorized as ‘advanced.’ For example, if a student-athlete born in 2000 starts kindergarten at the age of five, her first year of university and first year of athletic eligibility would commence in the fall semester of 2018. She would then continue into her second, third, and fourth years of eligibility in the fall semesters of 2019, 2020, and 2021, respectively. If her actual and expected athletic eligibilities correspond this way, she is considered ‘on-time.’ However, if a student-athlete born in 2000 starts her first year of university and first year of athletic eligibility in the fall of 2019 or later, her actual and expected athletic eligibilities no longer coincide. In this case, the student-athlete would be categorized as ‘delayed.’ Lastly, if a student-athlete born in 2000 starts her first year of university and first year of athletic eligibility in the fall of 2017 or earlier, she would be categorized as ‘advanced.’
Student-athletes may voluntarily delay themselves by extending their high school education for an extra year, or by being ‘redshirted’ during their collegiate athletic careers. Being ‘redshirted’ allows student-athletes to practice with their teams but not play and, therefore, not use up a year of athletic eligibility (Chittle et al., 2016). Other reasons for delays may include taking a year off between high school and post-secondary education, failing or having to repeat a previous grade, or being held back by one’s parents before starting kindergarten (Dixon et al., 2013).
Glamser and Marciani (1992) realized the important connection between AT and the RAE when they studied football players in the NCAA. At first glance, it appeared there was an even distribution of the players’ birthdays throughout the year, suggesting little evidence of a RAE among the collegiate football players in their sample. However, after controlling for AT, on-time student-athletes were five times more likely to have been born in January, February or March than in October, November, or December, demonstrating strong evidence of a RAE among this sub-sample of athletes. Similar results were found in NCAA Division I basketball (Chittle et al., 2016), Canadian interuniversity ice hockey (Chittle et al., 2015), and NCAA Division I women’s softball (Dixon et al., 2013).
Cut-Off Dates
When conducting RAE research, it is critical to choose the correct cut-off date for analysis. The cut-off date is what determines the selection year and, if chosen incorrectly, can lead researchers to making Type I (a false positive finding) or Type II (a false negative finding) errors (Delorme & Champely, 2015). When Daniel and Janssen (1987) examined Major League Baseball (MLB) players from the 1984-85 season, they used a September 1 cut-off date and found no RAE present among the MLB players in their study. However, when (Thompson et al., 1991) reanalyzed Daniel and Janssen’s (1987) data using an August 1 cut-off date, a significant RAE was revealed, showing that MLB players were more commonly born in the first months of the selection year and fewer players were born in the latter months. Thompson et al. (1991) used August 1 for their analyses because it was the cut-off date used by Little League Baseball at the time when most MLB players would have been honing their talents as youths. Subsequent research by Dixon, Chittle and Horton (2015) verified the prevalence of the RAE among athletes who competed in the 2011 and 2012 Little League World Series using a May 1 cut-off date. Little League Baseball changed its cut-off date to May 1 in 2006, and again to January 1 as recently as 2018 to coincide with the cut-off date used by the International Baseball Federation (Dixon et al., 2015). Nevertheless, these studies highlight the importance of choosing an appropriate cut-off date to ensure possible RAEs are not masked by the context in which they are being examined.
To date, no known studies have examined the RAE in intercollegiate golf, or if a RAE is present among female golfers in any setting. Thus, the purpose of this study is to examine the RAE among male and female NCAA golfers, while controlling for the moderating effects of AT, using two contextually specific cut-off dates.
Methods
Participants
For this study, the top 600 ranked female and male NCAA golfers (based on Golfweek as of January 25, 2016) were examined. The birthdates and eligibility years of these student-athletes were collected from publicly available sources. In instances where birthdate information was not obtainable for particular golfers, they were removed, as we were unable to determine their relative ages. Ages for all golfers were calculated as of January 1, 2016.
Classification of Student-Athletes
Golfers were categorized based on their sex, athletic eligibility year, AT, birthplace, and birth quartile. For AT purposes, golfers were grouped as either on-time, delayed, or advanced, and for their birthplace, they were grouped as either born in the United States or internationally. In our study, on-time student-athletes in their first, second, third, and fourth years of athletic eligibility should have been born in 1997, 1996, 1995, and 1994, respectively. Delayed student-athletes were those born one or more years earlier than the years that corresponded with their athletic eligibility and advanced student-athletes were those born one or more years later than the years that corresponded with their athletic eligibility.
We tested two separate cut-off dates in this study, August 1 and January 1. August 1 was chosen because it was the cut-off date previously used by Côté et al. (2006) and is employed by the PGA Junior League. January 1 was also chosen because this is the cut-off date utilized by the United States Golf Association (USGA) for its junior golf competitions (except for the United States Junior Amateur, which utilizes the date of the tournament each year as the cut-off date) and the American Junior Golf Association (AJGA) (American Junior Golf Association, 2016; United States Golf Association, 2016). For both cut-off dates, student-athletes were grouped into the appropriate birth quartile to allow for separate analyses to be conducted. For the August 1 cut-off date, golfers born in August, September, and October were grouped in quartile one (Q1), while golfers born in November, December, and January were grouped in quartile two (Q2), and so forth. For the January 1 cut-off date, Q1 included golfers born in January, February, and March, while Q2 comprised golfers born in April, May, and June, and so forth.
Data Analysis
Ideally, when examining student-athletes from only one country, such as the United States, we would be able to use census data to determine the exact distribution of births across quartiles for that country’s population and reduce the likelihood of making a Type I error (Delorme & Champely, 2015). However, due to the inclusion of international student-athletes, an equitable distribution of births across quartiles (i.e., 25%) was used for our comparisons, because in different countries the birthrates may vary by quartile. Based on an equal distribution, chi-square goodness of fit tests (X2) with a p < .05 level of significance were performed on the overall samples of male and female golfers for each cut-off date. Similar tests were also performed on the sub-samples of on-time and delayed golfers for each cut-off date. Advanced golfers were not included because their sample sizes were too small to ensure adequate power.
Small (0.1), medium (0.3), and large (0.5) effect sizes were calculated by using Cramer’s phi (φ). Post-hoc standardized residuals were also calculated on the chi-square values that were significant to determine which birth quartiles were significantly different from the expected birth distribution. Using p < .05 as the significance level, standardized residuals greater than 1.96 indicated an over-representation of births within a particular quartile, while standardized residuals less than -1.96 indicated an under-representation of births within a particular quartile. All statistical analyses were performed using the Statistical Package for the Social Sciences (SPSS).
Results
For our study, the birthdates of 284 female (x̄age = 21.12 years, sage = 1.36) and 309 male (x̄age = 21.44 years, sage = 1.33) student-athletes from among the top 600 ranked male and female NCAA golfers were obtained from publicly available sources. Of the female golfers, 168 (59.15%) were born in the United States and 116 (40.85%) were born abroad. Regarding the male sample, 215 (69.58%) were born in the United States and 94 (30.42%) were born internationally.
When examining the female sample, 148 (52.11%) of the student-athletes were on-time, 128 (45.07%) were delayed, and 8 (2.82%) were advanced. Of the on-time female golfers, 69.59% (n = 103) were born in the United States and 30.41% (n = 45) were born internationally. For the delayed female golfers, 48.44% (n = 62) were born in the United States and 51.56% (n = 66) were born outside of the United States. Of the advanced female golfers, 37.5% (n = 3) were born in the United States and 62.5% (n = 5) were born outside of the United States. In reference to the male sample, 124 (40.13%) of the student-athletes were on-time, 181 (58.58%) were delayed, and 4 (1.29%) were advanced. Of the on-time male golfers, 76.61% (n = 95) were born in the United States and 23.39% (n = 29) were born internationally. For the delayed male golfers 64.09% (n = 116) were born in the United States and 35.91% (n = 65) were born outside of the United States. Finally, for the advanced male golfers, 100% (n = 4) were born in the United States.
August 1 Analyses
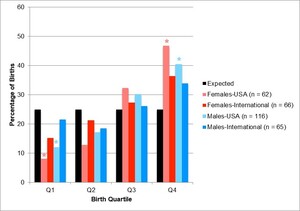
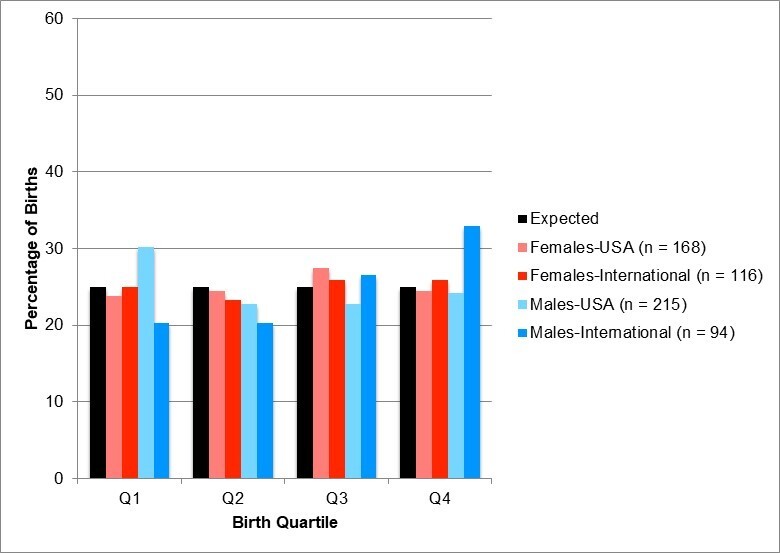
When examining our overall results using an August 1 cut-off date, no significant differences were revealed across birth quartiles for American born male (X2 = 1.91, df = 3, p = 0.59, φ = 0.09) or female (X2 = 3.57, df = 3, p = 0.31, φ = 0.15) golfers. Similarly, no significant differences were found across birth quartiles for the internationally born male (X2 = 1.83, df = 3, p = 0.61, φ = 0.14) or female (X2 = 3.38, df = 3, p = 0.34, φ = 0.17) golfers (see Figure 1 and Table 1). To discover if AT had an impact on the RAE for intercollegiate golfers, on-time and delayed student-athletes were analyzed separately. For on-time student-athletes, significant chi-square tests were revealed among American born male (X2 = 19.99, df = 3, p < 0.01, φ = 0.46) and female (X2 = 9.66, df = 3, p = 0.02, φ = 0.31) golfers (see Figure 2 and Table 2). For delayed student-athletes, significant chi-square tests were also revealed for American born male (X2 = 11.45, df = 3, p = 0.01, φ = 0.31) and female (X2 = 13.74, df = 3, p < 0.01, φ = 0.47) golfers, as well as for the internationally born female (X2 = 7.82, df = 3, p = 0.05, φ = 0.34) golfers (see Figure 3 and Table 3). Even though significant differences were found for on-time and delayed American born male and female golfers, and delayed internationally born female golfers, there were no distinguishable RAE patterns within these birth distributions.
January 1 Analyses
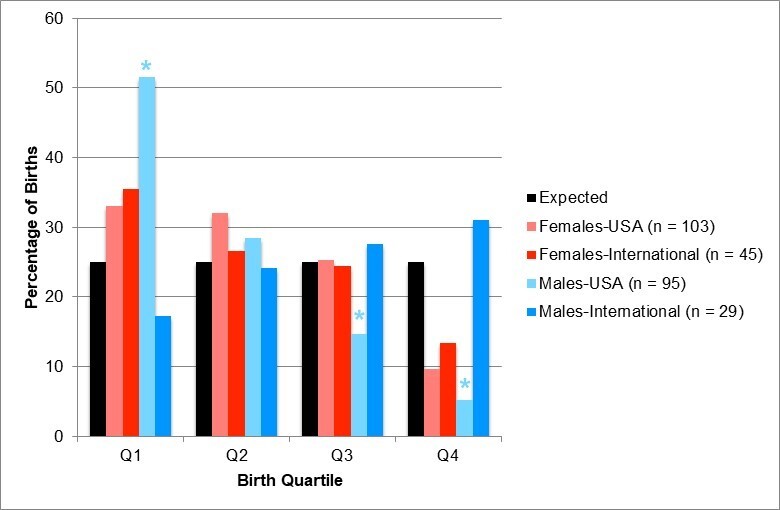
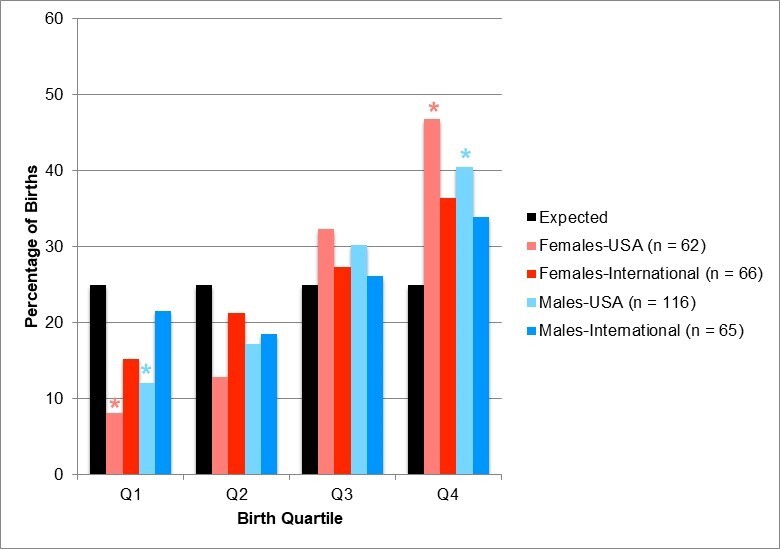
When examining our overall samples of student-athletes using a January 1 cut-off date, no significant differences were found across birth quartiles for American born male (X2 = 3.25, df = 3, p = 0.35, φ = 0.12) or female (X2 = 0.52, df = 3, p = 0.91, φ = 0.06) golfers, or internationally born male (X2 = 4.21, df = 3, p = 0.24, φ = 0.21) or female (X2 = 0.21, df = 3, p = 0.98, φ = 0.04) golfers (see Figure 4 and Table 1). Once again, the on-time and delayed student-athletes were analyzed separately to discern if AT has an impact on the RAE for intercollegiate golfers. For both on-time American born male and female golfers, strong evidence of a RAE was revealed (females: X2 = 14.32, df = 3, p < 0.01, φ = 0.37; males: X2 = 45.10, df = 3, p < 0.001, φ = 0.70). For the on-time American born male golfers, there were significantly more student-athletes born in Q1 than expected, whereas there were significantly fewer student-athletes born in Q3 and Q4. For the on-time American born female golfers, there were significantly fewer student-athletes born in Q4 than anticipated (see Figure 5 and Table 2). A significant inverse of the RAE was also discovered among delayed American born male and female student-athletes (females: X2 = 23.81, df = 3, p < 0.01, φ = 0.62; males: X2 = 22.97, df = 3, p < 0.01, φ = 0.44). For both the delayed American born male and female golfers, there were significantly fewer student-athletes born in Q1 and signficantly more student-athletes born in Q4 than in the expected distribution. (see Figure 6 and Table 3).
Discussion
For both cut-off dates, August 1 and January 1, the overall distribution of birthdates yielded no significant results or RAEs. Once we accounted for AT, significant chi-square tests and RAE trends were revealed. For the August 1 cut-off date, significant chi-square tests were found for American born on-time and delayed male and female student-athletes, as well as internationally born delayed female athletes. Despite these significant differences, no discernible RAE patterns were found within these birth distributions. However, when using the January 1 cut-off date, on-time golfers demonstrated a traditional RAE trend (aside from internationally born male and female student-athletes). For the American born male and female delayed student-athletes, a reverse RAE trend was also present.
Within our study, we found both the impact of AT and the choice of cut-off date critical to understanding the impact of the RAE among NCAA golfers. Côté et al. (2006) based their decision to use August 1 as their cut-off date on the fact that the United States National Junior Championship is usually held in the last two weeks of July. The PGA Junior League also uses August 1 as its cut-off date, as it coincides with the end of its regular season (PGA Junior League Golf, 2016). However, this cut-off date could be less relevant for studying the RAE among intercollegiate golfers because the USGA and AJGA use January 1 as their cut-off date. Thus, if January 1 is more commonly used as the cut-off date for junior golf competitions throughout the United States, using alternative dates such as August 1 to group athletes for RAE investigations could mask its prevalence.
Since no RAE trend appears among the overall samples of student-athletes for either the August 1 or January 1 cut-off dates, the NCAA may have inadvertently found a solution to the participation bias that can be associated with relative age. By delaying their entrance to post-secondary education, relatively younger student-athletes may be able to equalize the playing field with their relatively older golfing counterparts. However, this method will not be effective if large numbers of relatively older student-athletes also choose to delay their entrance into university.
Limitations and Future Directions
The first limitation is that we were unable to locate and verify the birthdates for many of the student-athletes ranked among the top 600 male and female NCAA golfers. Since birthdate information was collected from varsity athletic programs’ websites, the completeness and accuracy of our data are a function of the people who populated these websites. Nevertheless, any such errors are anticipated to be rare and occurring at random, thereby having little impact on the results of these analyses. In addition, we delimited our sample to the top 600 male and female NCAA golfers because this information was readily available. If the population data for all NCAA golfers were to become accessible, this would be a preferable future direction.
The second limitation pertains to the uncertainty about why student-athletes were delayed in their athletic eligibilities. In our study, 45.07% of female golfers and 59.58% of male golfers were delayed. It would be beneficial to determine why these athletes were delayed, and if they were purposely doing so to gain a competitive advantage. Future studies ought to explore these issues via interviews and/or focus groups with delayed student-athletes. However, this information would need to be collected through qualitative research, which was not within the scope of this study.
The third limitation of this study was the challenge associated with selecting the appropriate cut-off date(s) to use when analyzing our data. The January 1 and August 1 cut-off dates were chosen because of their use by prominent amateur golf organizations in the United States. However, these cut-off dates could differ from those employed in the various countries from which the internationally born student-athletes in this study were derived. This may help to explain why we found no significant differences among birth quartiles within the internationally born samples of student-athletes in this study.
The final limitation relates to our use of an expected birth distribution of 25% in each quartile. Since golfers from multiple countries were included in this study, the population birthdates may vary by quartile from country to country. By using an equal distribution instead of actual birth frequencies within the parent populations, there is the possibility for bias within our goodness-of-fit tests (Delorme & Champely, 2015). To prevent this bias in future studies, it may be beneficial to use the birth distributions of the general student population attending NCAA member institutions. Unfortunately, this information was not readily available at the time of our analysis.
Conclusion
The RAE explains the relative (dis)advantages individuals face because of where their birthdate falls compared to a pre-determined cut-off date. From the results of this study, it was found to be advantageous to be born in the months immediately following the January 1 cut-off date to compete in NCAA golf. However, consideration of AT was critical in coming to this conclusion. Without accounting for AT, one could be led to the misconception that no RAE exists among NCAA golfers. In separate examinations of on-time and delayed student-athletes using a January 1 cut-off date, we uncovered traditional RAEs within the on-time samples and inverse RAEs with the delayed samples for American born male and female golfers. In contrast, no RAEs were found when the data were analyzed using an August 1 cut-off date. Thus, the results of this study demonstrate the importance of determining the correct cut-off date when testing for RAEs, as incorrect cut-off dates can lead researchers to making statistical errors.
Given that no RAE was present in our overall samples of intercollegiate golfers, the NCAA may have unwittingly found a solution for this systematic bias. By delaying entrance to university, relatively younger student-athletes can create a more equal playing field with their relatively older counterparts. This practice seems to be commonplace among intercollegiate golfers, as 45.07% of female and 59.58% of male student-athletes in our study were delayed. This is important information for coaches and sport administrators to consider as they select teams or adapt their eligibility policies. This research adds more knowledge and understanding to the impact that RAEs and AT can have within sport and can, hopefully, help to create equal sporting opportunities for relatively older and younger athletes alike in the future.